| Auger recombination
processes in semiconductor heterostructures
Two recombination processes are predominant in semiconductors at high excitation levels:
related to the electron-electron interaction. While there have been published a lot of papers on calculation of radiative recombination (see for example [1,2]), there is no comprehensive and reliable theory predicting Auger recombination rate in semiconductor heterostructures until now. For the homogeneous case, mechanisms of Auger recombination have been extensively studied [1-6]. There are two main AR mechanisms in narrow gap semiconductors schematically shown below: CHCC process and CHHS process [1,4,6]. Both these processes are of threshold nature, and the rate of Auger recombination changes with temperature exponentially [3,4]. 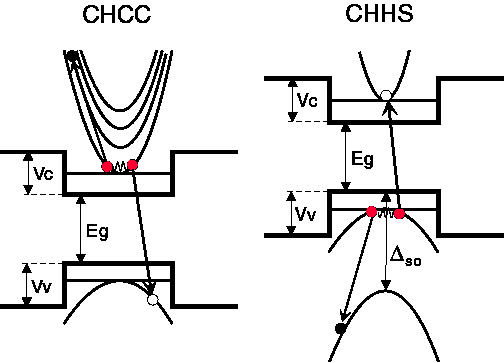 CHCC, CHHS Auger process in a quantum well. Single semiconductor heterostructures: quantum wells, quantum wires, quantum dots are spatially inhomogeneous owing to the existence of barriers. The presence of a heteroboundary affects not only the energy and wave functions of carriers, but also the macroscopic properties of heterostructures [7], which is of primary importance. It is commonly believed that the AR mechanism in quantum wells is the same as in a homogeneous semiconductor [1,2,8-10]. Nevertheless, the presence of a heteroboundary strongly affects the electron-electron interaction in quantum wells, and this influence is of fundamental nature. The heteroboundary lifts restrictions imposed on processes of electron-electron interaction by the energy and momentum conservation laws. Namely, the conservation of quasi-momentum perpendicular to the heteroboundary breaks down. In turn, this leads to the appearance in heterostructures of new thresholdless channels of Auger recombination [7]. The rate of the thresholdless AR process is a power function of temperature. The first direct experiment aimed at observing the thresholdless AR channel at T=77K was reported in [10]. Recently there have been discovered the thresholdless nature of AR in type-II uantum wells [12]. At low temperature the thresholdless process, in contrast to the threshold one, is rather an efficient channel of nonradiative recombination, and for narrow quantum wells and high concentrations it dominates the phonon-assisted AR process. The existence of a thresholdless matrix element of electron-electron interaction also exerts strong influence on the phonon-assisted AR process. The latter becomes resonant and is much enhanced as compared with the 3D phonon-assisted Auger process [13]. A detailed analysis of the threshold and thresholdless AR mechanisms has been performed for a single heterobarrier [7]. Conditions were studied under which the thresholdless channel dominates over the threshold one. For quantum wells no such detailed analysis has been done. Taylor et al. [14] considered the possibility of removing the threshold for AR in quantum wells upon transition of excited carriers to the continuos part of spectrum. However, no microscopic theory of the thresholdless process was given in this work and no theoretical analysis performed of the competition between the threshold, quasi-threshold, and thresholdless AR mechanisms at various temperatures and quantum well widths. Only the thresholdless AR channel, corresponding to small momenta transferred in Coulomb interaction of particles (for the CHCC process) with spin-orbit interaction neglected, was considered in [15,16]. A detailed analysis of AR recombination in Quantum Wells have been recently developed by us [13,17]. It was shown that there exist three fundamentally different AR mechanisms: (i) threshold mechanism similar to an Auger process in a homogeneous semiconductor, (ii) quasi-threshold mechanism with a threshold energy strongly depending on the quantum well width, and (iii) thresholdless mechanism inoperative in a homogeneous semiconductor. For the threshold AR process in a quantum well the threshold energy is close to that in a homogeneous semiconductor. Conversely, owing to the small value of the threshold energy, the rate of the quasi-threshold process in narrow quantum wells depends on temperature only slightly. For this reason there is no clear distinction between mechanisms (ii) and (iii) in sufficiently narrow quantum wells, and they may be considered as a single thresholdless AR process. With increasing quantum well width, the threshold energy of the quasi-threshold process increases and approaches the bulk value. A totally different behavior is characteristic of the thresholdless AR mechanism. With increasing quantum well width, its rate falls dramatically and, on passing to a homogeneous semiconductor, this mechanism ceases to be operative. Here we offer results of calculation of AR coefficient for a number of semiconductor heterostructures with quantum wells often used in optoelectronic devices. Our main goal is to investigate principle dependences of the coefficient on temperature and parameters of the quantum well rather than to calculate the coefficient with high accuracy. Therefore an approximate expressions for the AR coefficient were used. Nevertheless these expressions qualitatively reflect basic features of AR process behavior with change of temperature and parameters of a quantum well. Reference
|