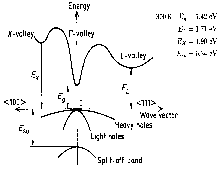
Eg = 1.42 eV
EL = 1.71 eV
EX= 1.90 eV
Eso = 0.34 eV

| Energy gap | 1.424 eV |
| Energy separation (EΓL) between Γ and L valleys | 0.29 eV |
| Energy separation (EΓX) between Γ and X valleys | 0.48 eV |
| Energy spin-orbital splitting | 0.34 eV |
| Intrinsic carrier concentration | 2.1·106 cm-3 |
| Intrinsic resistivity | 3.3·108 Ω·cm |
| Effective conduction band density of states | 4.7·1017 cm-3 |
| Effective valence band density of states | 9.0·1018 cm-3 |
 |
Band structure and carrier concentration of GaAs. 300 K Eg = 1.42 eV EL = 1.71 eV EX= 1.90 eV Eso = 0.34 eV |
Eg=1.519-5.405·10-4·T2/(T+204) (eV)
where T is temperatures in degrees K (0 < T < 103).
Temperature dependence of the energy difference between the top of the valence band and the bottom of the L-valley of the conduction band
EL=1.815-6.05·10-4·T2/(T+204) (eV)
Temperature dependence of the energy difference between the top of the valence band and the bottom of the X-valley of the conduction band
EL=1.981-4.60·10-4·T2/(T+204) (eV)
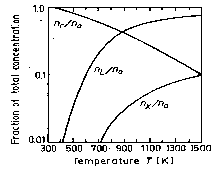 |
The temperature dependences of the relative populations of the Γ, L and X valleys. (Blakemore [1982]). |
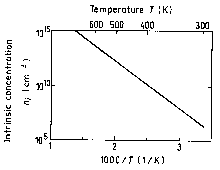 |
The temperature dependences of the intrinsic carrier concentration. (Shur [1990]). |
ni =(Nc ·Nν )1/2exp(-Eg/(2kbT))
Effective density of states in the conduction band taking into account the nonparabolicity of the Γ-valley and contributions from the X and L-valleys
Nc= 8.63·1013·T3/2[1-1.9310-4·T-4.19·10-8·T2 +21·exp(-EΓL/(2kbT))
+44·exp(-EΓX/(2kbT)) (cm-3)
Nv= 1.83·1015·T3/2(cm-3)
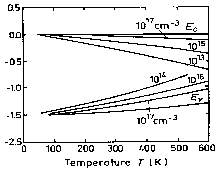 |
Fermi level versus temperature for different concentrations of shallow donors and acceptors. |
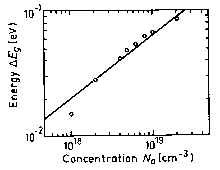 |
Energy gap narrowing at high doping levels. (Tiwari and Wright [1990]) |
ΔEg ≈ 2·10-11·Na-1/2 (eV) (Na- in cm.-3)
| For Γ-valley | mΓ = 0.063mo |
| In the L-valley the surfaces of equal energy are ellipsoids | |
| ml= 1.9mo | |
| mt= 0.075mo | |
| Effective mass of density of states | |
| mL=(16mlmt2)1/3 | mL=0.85mo |
| In the X-valley the surfaces of equal energy are ellipsoids | |
| ml= 1.9mo | |
| mt= 0.19mo | |
| Effective mass of density of states | |
| mX=(9mlmt2)1/3 | mX=0.85mo |
| Heavy | mh = 0.51mo |
| Light | mlp = 0.082mo |
| Split-off band | mso = 0.15mo |
| Effective mass of density of states | mv = 0.53mo |
| S | Se | Si | Ge | Sn | Te |
| ~0.006 | ~0.006 | ~0.006 | ~0.006 | ~0.006 | ~0.03 |
| C | Si | Ge | Zn | Sn |
| ~0.02 | ~0.03/0.1/0.22 | ~0.03 | ~0.025 | ~0.2 |