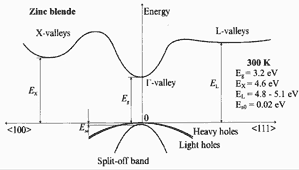
300K; Eg =3.2 eV eV; EX= 4.6 eV; EL= 4.8-5.1 eV; Eso = 0.02 eV
For details see Suzuki, Uenoyama & Yanase (1995) .
| Remarks | Referens | ||
| Energy gaps, Eg |
3.28 eV | 0 K | Bougrov et al. (2001) | Energy gaps, Eg |
3.2 eV | 300 K |
| Electron affinity | 4.1 eV | 300 K | |
| Conduction band | |||
| Energy separation between Γ valley and X valleys EΓ | 1.4 eV | 300 K | Bougrov et al. (2001) |
| Energy separation between Γ valley and L valleys EL | 1.6 ÷ 1.9 eV | 300 K | |
| Effective conduction band density of states | 1.2 x 1018 cm-3 | 300 K | |
| Valence band | |||
| Energy of spin-orbital splitting Eso |
0.02 eV |
300 K | |
| Effective valence band density of states | 4.1 x 1019 cm-3 | 300 K |
| Remarks | Referens | ||
| Energy gaps, Eg | 3.47 eV | 0 K | Bougrov et al. (2001) |
| 3.39 eV | 300 K | Chow & Ghezzo (1996) | |
| Energy gaps, Eg,dir | 3.503 (2) eV | 1.6 K; photoluminescence, from excitonic gap adding the exciton binding energy |
Monemar (1974) |
| 3.4751(5) eV | 1.6 K; A-exciton (transition from Γ9v) | ||
| 3.4815(10) eV | 1.6 K; B-exciton (transition from upper Γ7v) | ||
| 3.493 (5) eV | 1.6 K; C-exciton (transition from lower Γ7v) | ||
| 3.44 eV | 300K; temperature dependence below 295 K given by: Eg(T) - Eg(0) = - 5.08 x 10-4 T2/(996 - T), (T in K) . see also Figure "Band gap energy and exciton energies vs. temperature" |
Madelung (1991) | |
| Electron affinity | 4.1 eV | 300 K | Bougrov et al. (2001) |
| Remarks | Referens | ||
| Conduction band | |
||
| Energy separation between Γ valley and M-L valleys | 1.1 ÷ 1.9 eV | 300 K | Bougrov et al. (2001) |
| Energy separation between M-L-valleys degeneracy | 6 eV | 300 K | |
| Energy separation between Γ valley and A valleys | 1.3 ÷ 2.1 eV | 300 K | |
| Energy separation between A-valley degeneracy |
1 eV |
300 K | |
| also The energy separations between the Γ9
state and the two Γ 7 states can be calculated from the energy separations of the A-, B-, C-excitons. |
Madelung (1991) | ||
| Effective conduction band density of states | 2.3 x 1018 cm-3 | 300 K | |
| Valence band | |||
| Energy of spin-orbital splitting Eso | 0.008 eV | 300 K | Bougrov et al. (2001) |
| Energy of spin-orbital splitting Eso | 11(+5,-2) meV | 300 K; calculated from the values of energy gap Eg,dir (given above) |
Dingle & Ilegems (1971) |
|
Energy of crystal-field splitting Ecr |
0.04 eV | 300 K | Bougrov et al. (2001) |
|
Energy of crystal-field splitting Ecr |
22(2) meV | 300 K; calculated from the values of energy gap Eg,dir (given above) |
Dingle & Ilegems (1971) |
|
Effective valence band density of states |
4.6 x 1019 cm-3 | 300 K | |
 |
Band structure of zinc blende(cubic) GaN. Important minima of the
conduction band and maxima of the valence band. 300K; Eg =3.2 eV eV; EX= 4.6 eV; EL= 4.8-5.1 eV; Eso = 0.02 eV For details see Suzuki, Uenoyama & Yanase (1995) . |
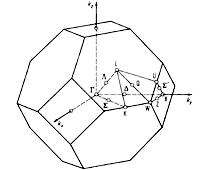 |
Brillouin zone of the face centered cubic lattice, the Bravais lattice of the diamond and zincblende structures. |
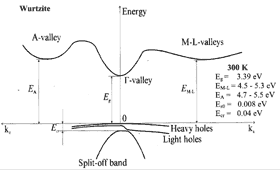 |
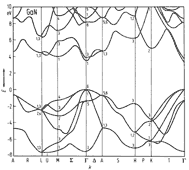
GaN, Wurtzite. Band structure. Important minima of
the conduction band and maxima of the valence band. Valence band 3 splitted
bands. This splitting results from spin-orbit interaction and from crystal
symmetry. 300K; Eg =3.39 eV eV; EM-L= 4.5-5.3 eV; EA= 4.7-5.5 eV; Eso = 0.008 eV; Ecr = 0.04 eV For details see Suzuki, Uenoyama & Yanase (1995) . |
 |
GaN, Wurtzite. Band structure calculated with an empirical
pseudopotential method The band structure differs only slightly from other spin-neglecting calculations. Introduction of spin-orbit interaction leads to a splitting of the uppermost valence band at Γ from Γ1 + Γ6 , into Γ9 + Γ7 + Γ7 . The energy differences between these terms can be described by two parameters - the spin-orbit splitting energy Eso (Δso) and the crystal field splitting energy Ecr(Δcr). Also see Basic Parameters. Bloom et al.(1974) |
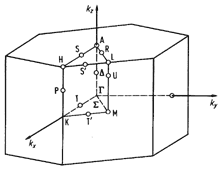 |
Brillouin zone of the hexagonal lattice. |
| Eg = Eg(0) - 7.7·10-4x
T2/(T + 600) |
(eV) | Bougrov et al. (2001 |
| Eg(0) = 3.47 eV (wurtzite)
Eg(0) = 3.28 eV (zinc blende) |
||
| Eg = Eg(0) - 9.39 x 10-4
x T2/(T + 772) |
(eV) | Guo & Yoshida (1994) Teisseyre al. (1994) |
| Eg (0 K) = 3.427 eV |
| Varshni expression: | ||
| Eg = Eg(0) - 9.39·10-4x T2/(T + 772) | (eV) | Guo & Yoshida (1994),
Teisseyre al. (1994) |
| where Eg(0) = 3.427 eV and T is temperature in degrees K |
 |
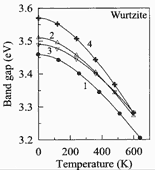
GaN, Wurtzite. Band gap energy and exciton energies vs. temperature Monemar (1974) Temperature dependence below 295 K given by: Eg(T) - Eg(0) = - 5.08 x 10-4 T2/(996 - T), (T in K). Eg(300K) =3.44 eV |
 |
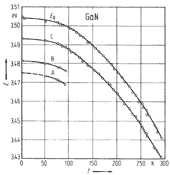
GaN, Wurtzite. Band gap energy versus temperature. GaN samples
were grown on different substrates using different techniques. Experimental
data are taken from four different works. Bougrov et al. (2001) |
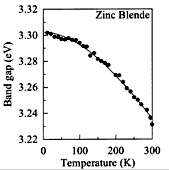 |
GaN, Zinc Blende(cubic). The Band gap energy versus temperature.
GaN films were grown on MgO (1x1) substrates. Ramirez-Flores et al. (1994) |
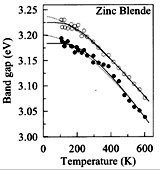 |
GaN, Zinc Blende(cubic). The Band gap energy versus temperature.
GaN films were grown on Si (100) substrates. The dependences were extracted
from pseudodielectric-function spectrum using two different theoretical
models Petalas et al. (1995) |
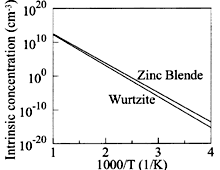 |
GaN, Wurtzite & Zinc Blende. The intrinsic carrier concentration
vs. temperature. Bougrov et al. (2001) |
| AIN/GaN(0001) | Referens | |
| Conduction band discontinuity | ΔEc = 2.0 eV | Martin et al. (1996) |
| Valence band discontinuity | ΔEv = 0.7 eV | |
| InN/GaN | ||
| Conduction band discontinuity | ΔEc = 0.43 eV | Martin et al. (1996) |
| Valence band discontinuity | ΔEv = 1.0 eV |
| GaAs/GaN | Referens | |
| Valence band discontinuity | ΔEv = 1.84 eV | Ding et al. (1997) |
| Effective Masses for Zinc Blende GaN | Remarks | Referens | |
| Effective electron mass me | 0.13 mo | 300 K | Bougrov et al. (2001) |
| Effective Masses for Wurtzite GaN | |||
| Effective electron mass me | 0.20 mo | 300 K | Bougrov et al. (2001) |
| 0.27 (6) mo | 300K; Faraday rotation | Rheinlander & Neumann (1974) | |
Effective electron mass me
|
0.20(2) mo | 300K; fit of reflectance spectrum | Bloom et al.(1973) |
| Effective electron mass me|| | 0.20(6) mo |
| Effective Masses for Zinc Blende GaN | Remarks | Referens | |
| Effective mass of density of state mv | mv = 1.4 mo | ||
| Effective hole masses (heavy) mhh | mhh = 1.3 mo m[100] = 0.8 mo m[111] = 1.7 mo |
300 K | Leszczynski et al. (1996), Fan et al. (1996) |
| Effective hole masses (light) mlp | mlh = 0.19mo m[100] = 0.21 mo m[111] = 0.18 mo |
300 K | |
| Effective hole masses (split-off band) ms | msh = 0.33 mo m[100] = 0.33 mo m[111] = 0.33 mo |
300 K |
| Effective Masses for Wurtzite GaN | Remarks | Referens | |
| Effective mass of density of state mv | 1.5 m0 | Leszczynski et al. (1996), Fan et al. (1996) |
|
| Effective hole masses | 0.8 (2) mo | 300 K, experimental | Pankove et al.(1975) |
| Effective hole masses (heavy) mhh | mhh = 1.4 mo mhhz = 1.1 mo mhh 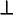 = 1.6 mo = 1.6 mo |
300 K; calculated values | Leszczynski et al. (1996), Fan et al. (1996) |
| Effective hole masses (light) mlp | 0.259 mo | 300 K; calculated values |
|
| Effective hole masses (light) | mlh = 0.3 mo mlhz = 1.1 mo mlh 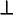 = 0.15 mo = 0.15 mo |
300 K; calculated values | Leszczynski et al. (1996), Fan et al. (1996) |
| Effective hole masses (split-off band) ms | msh = 0.6 mo mshz = 0.15 mo msh 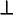 = 1.1 mo = 1.1 mo |
300 K; calculated values | Leszczynski et al. (1996), Fan et al. (1996) |
| Ionization energies of Shallow Donors |
||
| Si |
0.12-0.02 eV |
Bougrov et al. (2001) |
| Native defect level VN |
0.03 eV |
|
| Ionization energies of Shallow Acceptor |
||
| Mg |
0.14-0.21 eV |
Strite & Morkoc (1992), Akasaki & Amano (1994b) |
| Zn |
0.21 eV |
|
| Native defect level VGa |
0.14 eV |
| Ipurity or Defect | Ga Site | N Site | Referens |
| Si | 0.12-0.02 eV | Bougrov et al. (2001) | |
| VN (vacancy) | 0.03; 0.1 eV | ||
| C | 0.11-0.14 eV | ||
| Mg | 0.26; 0.6 eV |
| Ipurity or Defect | Ga Site | N Site | Referens |
| VGa (vacancy) | 0.14 | Bougrov et al. (2001) | |
| Mg | 0.14-0.21 eV | ||
| Si | 0.19 eV | ||
| Zn | 0.21-0.34 eV | ||
| Hg | 0.41 eV | ||
| Cd | 0.55 eV | ||
| Be | 0.7 eV | ||
| Li | 0.75 eV | ||
| C | 0.89 eV | ||
| Ga | 0.59-1.09 eV |