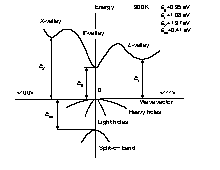
Important minima of the conduction band and maxima of the valence band.
Eg= 0.35 eV
EL= 1.08 eV
EX= 1.37 eV
Eso = 0.41 eV
| Energy gap | 0.354 eV |
| Energy separation (EΓL) between Γ and L valleys | 0.73 eV |
| Energy separation (EΓX) between Γ and X valleys | 1.02 eV |
| Energy spin-orbital splitting | 0.41 eV |
| Intrinsic carrier concentration | 1·1015 cm-3 |
| Intrinsic resistivity | 0.16 Ω·cm |
| Effective conduction band density of states | 8.7·1016 cm-3 |
| Effective valence band density of states | 6.6·1018 cm-3 |
 |
Band structure and carrier concentration of InAs. Important minima of the conduction band and maxima of the valence band. Eg= 0.35 eV EL= 1.08 eV EX= 1.37 eV Eso = 0.41 eV |
Eg = 0.415 - 2.76·10-4·T2/(T+83) (eV),where T is temperature in degrees K (0 <T < 300).
Nc≈1.68·1013·T3/2 (cm-3).
Nv≈ 1.27·1015·T3/2(cm-3).
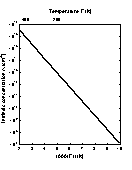 |
The temperature dependences of the intrinsic carrier concentration. |
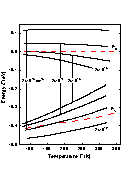 |
Fermi level versus temperature for different concentrations of shallow donors and acceptors. |
Eg≈Eg(0) + 4.8·10-3P (eV)where P is pressure in kbar (Edwards and Drickamer[1961]).
EL≈ EL(0) + 3.2·10-3P (eV)
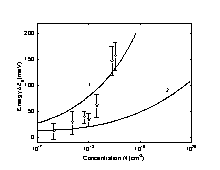 |
Energy gap narrowing versus donor (Curve 1) and acceptor (Curve 2 ) doping density. Curves are calculated according (Jain et al. [1990]). Points show experimental results for n-InAs (Semikolenova et al. [1978]). |
ΔEg = 14.0·10-9·Nd1/3 + 1.97·10-7·Nd1/4 + 57.9·10-12·Nd1/2 (eV)(Jain et al. [1990])
ΔEg = 8.34·10-9·Na1/3 + 2.91·10-7·Na1/4 + 4.53·10-12·Na1/2 (eV)(Jain et al. [1990])
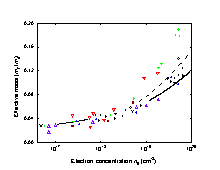 |
Electron effective mass versus electron concentration (Kesamanly et al. [1969]). |
| For Γ-valley | mΓ = 0.023mo |
| Nonparabolicity: E(1+αE) = h2k2/(2mΓ) |
α = 1.4 (eV-1) |
| In the L-valley effective mass of density of states | mL=0.29mo |
| In the X-valley effective mass of density of states | mX=0.64mo |
Heavy |
mh = 0.41mo |
Light |
mlp = 0.026mo |
Split-off band |
mso = 0.16mo |
| Sn | Ge | Si | Cd | Zn |
| 0.01 | 0.014 | 0.02 | 0.015 | 0.01 |