|
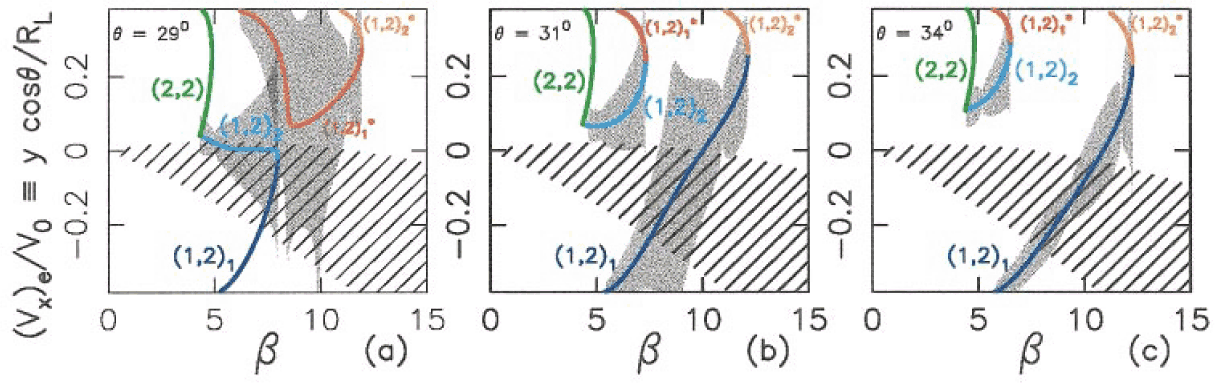
Bifurcation diagrams for the four period-two orbits relevant to the peak doubling in the interval u
q = 29° - 34°
(see text). Colored lines indicate y coordinate of the single collision with the emitter; these lines coincide at bifurcations.
q = 29°
(a) indicates behavior before the exchange bifurcation; q = 31° ( b) and 34° (c) after.
Shading represents the localization lengths lm associated with the relevant orbits [(1,2)2 and (1,2)1 for (a),
and (1,2)2* and (1,2)1 for (b), (c)]. Hatched region denotes semiclassical
width of emitter state; overlap indicates a large contribution to the tunneling current.
|
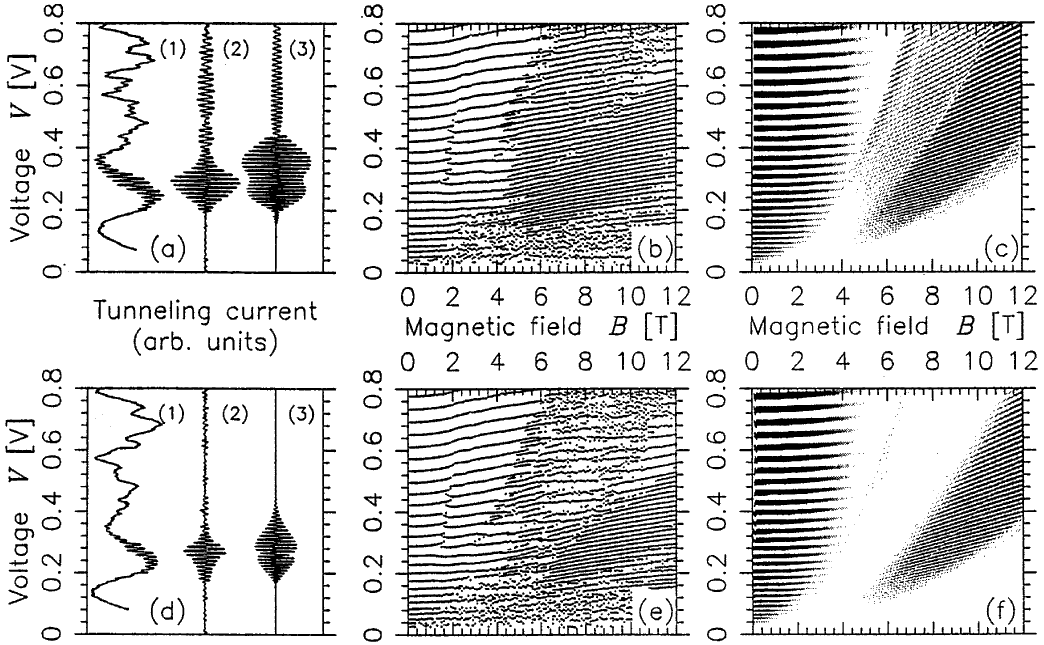
|
(a),(d): Resonant tunneling I-V traces for q = 31°, q = 34° at B = 8 T.
Trace (1) is raw experimental data, trace (2) is same data, filtered to retain only period-two oscillations, trace (3) is semiclassical prediction.
The modest discrepancies in the shape of the envelope of the amplitude of the oscillations is due to the inaccuracy of the quadratic semiclassical theory near
the bifurcation which occurs around 0.3 V at 8 T.
(b),(e): Peak positions vs voltage and magnetic field, determined from multiple sets of experimental I-V data at q = 31°,34°.
(c),(f): Semiclassical I-V oscillations for same, note gray scale indicates relative
amplitudes, not just peak positions. Note disappearance of high voltage oscillations at q = 34° due to movement of (1,2)2 orbit
away from accessibility after the exchange bifurcation .
|

