Fundamental Physical Constants

Modern theories of fundamental intaractions (SUSY GUT, Superstring/M-theory and others) not only predict the dependence of fundamental physical constants on energy ("running" constants), but also have cosmological solutions in which low-energy values of these constants vary with the cosmological time.

The predicted variations at the present epoch are small but non-zero, and they depend on theoretical model used. Clearly, a discovery of these variations would be a great step in our understanding of Nature. Even a reliable upper bound on a possible variation rate of a fundamental constant presents an effective tool for selecting viable theoretical models.

The main attention we pay to the following constants:

the fine-structure constant	α = e2/ħc
proton-to-electron mass ratio	μ = mp/me

Different theoretical models of the fundamental physical interactions predict different variations of their values and different relations between cosmological deviations of the constants (α, μ, and others, see Calmet & Fritzsch hep-ph/0112110, Langacker et al. hep-ph/0112233 , Olive et al. hep-ph/0205269 , Dent & Fairbairn hep-ph/0112279 ). Therefore, it is crucial to couple measurement of different dimensionless fundamental constants.

Presently, the fundamental constants are being measured with a relative error of ~10^-8 (Physical Reference Data NIST). These measurements obviously rule out considerable variations of the constants on a short time scale, but do not exclude their changes over the entire lifetime of the Universe, ~1.5x10¹⁰ years. Moreover, one cannot rule out the possibility that the coupling constants differ in widely separated regions of the Universe; THIS COULD DE DISPROVED ONLY by EXPERIMENTS and OBSERVATIONS !

It is extremely difficult to increase the accuracy of the present-day experiments and trace possible variation of the fundamental constants during cosmological evolution of the Universe. Fortunately, Nature has provided us with a tool for direct measuring the physical constants in the early epoches. This tool is based on observations of quasars (QSO) - the most powerful source of radiation.

Many quasars belong to the most distant objects we can observe. Light from the distant quasars travels to us about 10¹⁰ years. This means that the quasar spectra registered now were formed ~10¹⁰ years ago. Because of the expansion of the Universe, distant objects recede from us at a great velocity. As a result, the wavelengths of the lines observed in spectra of these objects λ_obs increase compared to their laboratory values λ_lab in proportion λ_obs = λ_lab(1+z), where the cosmological redshift z can be used to determine the age of the Universe at the line-formation epoch.

Analyzing these spectra we may study the epoch when the Universe was several times younger than now. Thus, the quasar spectra are true keepers of the history of the Universe as its space-time photos.

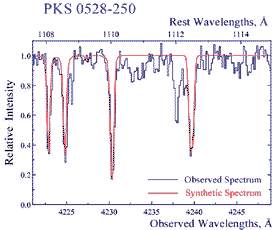
A new limit on the possible cosmological variation of the proton-to-electron mass ratio μ is estimated by measuring wavelengths of H₂ lines of Lyman and Werner bands from two absorption systems at z_abs = 2.5947 (profiles of the H₂ lines) and 3.0249 (profiles of the H₂ lines) in the spectra of quasars Q 0405-443 and Q 0347-383, respectively. Data are of the highest spectral resolution (R = 53000) and S/N ratio (30 - 70) for this kind of study. We search for any correlation between z_i, the redshift of observed lines, determined using laboratory wavelengths as references, and K_i, the sensitivity coefficient of the lines to a change of μ, that could be interpreted as a variation of μ over the corresponding cosmological time. We use two sets of laboratory wavelengths, the first one, Set (A) (H. Abgrall, E. Roueff, F. Launay, J.-Y. Roncin, & J.-L. Subtil, 1993, J. of Mol. Spec., 157, 512), based on experimental determination of energy levels and the second one, Set (P) (J. Philip, J.P. Sprengers, Th. Pielage, C.A. Lange, W. Ubachs, & E. Reinhold, 2004, Can. J. Chem., 82, 713), based on new laboratory measurements of some individual rest-wavelengths. We find Δμ/μ = ( 3.05 ± 0.75 )×10^-5 for Set (A), and Δμ/μ = ( 1.65 ± 0.74 )×10^-5 for Set (P). The second determination is the most stringent limit on the variation of μ over the last 12~Gyrs ever obtained. The correlation found using Set (A) seems to show that some amount of systematic error is hidden in the determination of energy levels of the H₂ molecule.