It is well known that primordial nucleosynthesis (Big Bang Nucleosynthesis, BBN) and cosmic microwave background radiation (CMBR) provide a unique window on the early Universe. They constitute two crucial quantitative tests of the standard big bang cosmological model. Indeed, BBN and CMBR, which have been related simbiotically from early works of the late 1940s, provide complementary views of the early Universe. The synthesis of the light elements is determined by events occuring in the epochs from ~1 to ~1000 s in the history of the Universe when temperatures varied from ~1010 K or higher to ~108 K. Thus, the observed abundances offer a probe of the Universe at epochs much earlier than those probed by CMBR (t~105 yr; T~104 K).
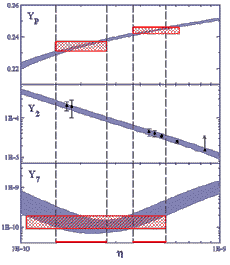
Detailed comparison of the predicted relative element abundances with the
observational data allows to test cosmological models and to obtain values
of their key parameters, such as average density of matter in the Universe,
baryon density, number of light neutrino species etc. Obviously, that to solve
the primordial nucleosynthesis problem is important not only for cosmology but
for elementary particle physics.
The standard Big Bang model of cosmology is the simplest (i.e., it has the fewest adjustable parameters), based on the observed large-scale isotropy and homogeneity of the Universe. In the framework of the general relativity it describe an expansion of self-gravitating medium under the assumption that physical laws at the nucleosynthesis epoch were the same as now. Utilizing only the known particles (e.g., assuming three species of light neutrinos), the nucleosynthesis predictions of the standard model depend on only one parameter, the ratio, h, of nucleons to photons (h= nb/ng) (or, equivalently, the density of baryons, since ng is known from measurements of the CMBR).
We have elaborated a new nucleosynthesis code independent of the standard code developed by Wagoner-Kawano. Certainly, the basic physics of the processes is the same as in the standard code but we have completely revised the integration routine, added new and updated nuclear reactions and specially designed it for the problem discussed.
The differential equations governing the light element abundances are stiff, thus the
special implicit methods of integration should be applied to accelerate the calculation process.
Instead of specifying explicit time steps, as it is done in the standard code, the desired
final accuracies are specified as parameters of our code integrator. The temperature steps
are then determined adaptively. Integrator accuracy parameters are chosen to be small enough
for stepsize errors to be much smaller than the allowed error of the 4He abundance. We have
worked out our code on Gear method (implicit multistep method of the variable order of
precision with an adaptive stepsize control).
To calculate weak interaction rates more accurately the eighth order Newton-Kotez routine is used. All the weak rates were calculated so that their numerical error contributions to the uncertainty in 4He abundance were acceptably small (in comparison with contribution of any other uncertainty).
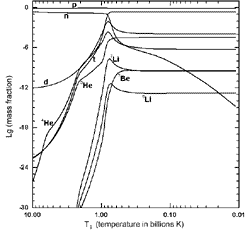
By now the code is implemented for 9 most light nuclides (protons, neutrons, D, T, 3He, 4He, 6Li, 7Li and 7Be); it includes the data on 39 nuclear reactions. The opportunity of direct change of input physical parameters is enclosed in the code within the framework of the existing theories.