Peculiarities of the space-time distribution
of absorption-line systems observed in QSO spectra
within a cosmological redshift
interval z=0.2-3.2 were analysed by
Ryabinkov et al. (1998, 1999)
and Kaminker et al. (2000).
The authors used the absorption lines
of the resonance doublets C IV and Mg II
as indicators of absorbing material existing at the
redshifts under study.
These spectral lines are usually observed in
QSO spectra with high emission-line redshift ze.
Results of the statistical analysis indicate that
the overall z-distribution of absorbing matter is non-uniform: it has statistically significant maxima (peaks) and minima (depressions), and
positions of peaks and depressions of the z-distribution turn out to be the same (within the statistical uncertainty) for different celestial hemispheres independently of their orientation.
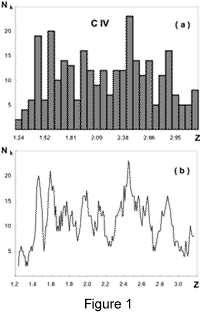
Figs. 1a and 1b show the z-distribution of the 299 C IV absorption systems. Fig. 1a is a histogram obtained for independent bins Dz=0.071. Fig. 1b presents the distribution obtained in so-called sliding-average approach, in which a set of consecutive shifts is performed of an averaging bin Dz = 0.071 along the z-axis with a step 0.01.
Positions
of the maxima (peaks) zm
were determined as weighted
mean values (centers of gravity)
of the points forming a peak
relative to the trend of the distribution
obtained in the sliding-average approach.
The corresponding values of zm are
1.46, 1.60, 1.78,
1.98, 2.14, 2.45, 2.64, and 2.86, with accuracy ±0.04
(half of the bin width).
The significance levels of the peaks
are estimated as 3s, 3s, s, 2s, s, 3s, 2s, 2s,
respectively.
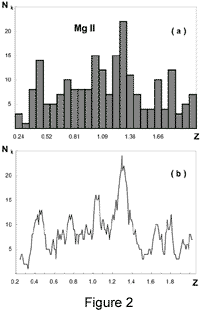
The results for Mg II absorption-line systems are quite consistent with the results discussed above. Figs. 2a and 2b show the z distribution of 216 Mg II absorption systems. The values of the centers of gravity of the peaks are equal zm= 0.44, 0.77, 1.04, 1.30, 1.66, and 1.78 (±0.04). The significance values of the peaks are 2s, s ,3s, 4s, s, s, respectively. One can see, that the last two peaks of Mg II systems are in a good agreement with the second and third peaks in the distribution of C IV systems.
Isotropy (or anisotropy)
of distributions was tested
by comparison of
the z-distributions
in opposite independent hemispheres.
For this purpose the celestial sphere was divided
(Equatorial coordinates) into
two hemispheres separated by the plane passing through the
world axis (d=±90°,
d is a declination).
This plane was rotated about the world axis
by steps Da=15° (1h),
where a is a right ascension.
For each hemisphere, it was produced the z-distribution
of the absorption systems.
A correlation coefficient r was calculated
for each pair of independent hemispheres
and comparison of values r
was performed with tabulated values
rb of the sample correlation coefficient
for a given confidence level b.
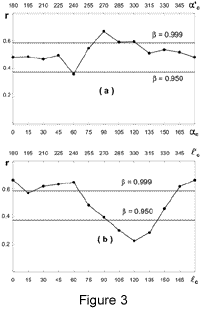
Fig. 3a represents the correlation coefficients for the z-distributions in pairs of opposite hemispheres as a function of the right ascensions of the centers of the hemispheres. It is clear that the correlation of the z-distributions is significant, as a rule, at the 2s level (b³0.95). To verify that the positions of the distribution maxima do not depend on an orientation of the rotation axis it was performed the procedure described above but with another rotation axis. The Galactic coordinates (l, b) (l and b are the Galactic longitude and latitude) were used instead of the Equatorial ones. Fig. 3b represents the correlation coefficients for the z-distributions as a function of the Galactic longitudes of the centers of the hemispheres.
In addition, possible regularity (periodicity) of the z-distribution obtained was tested within the total interval 0.2£z£3.2, exploring two independent methods:
regression analysis of the peak values zm, and
power spectrum analysis of the available sample of redshifts.
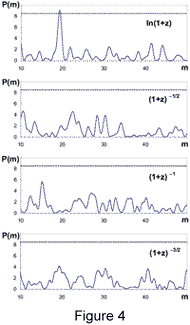In particular, the results of the power spectrum analysis
for four trial functions
are represented in Fig. 4.
One can see that
in the interval of m considered
the only significant peak of P(m) appears
for the function
f(z)=ln(1+z) at m=19 on the confidence level
b=0.99989 . This peak corresponds to
a periodicity of the distribution
in respect to this function with a period
D=F/m=0.066 ±0.003.
This is quite consistent with the results of the
regression analysis mentioned above.
Let us note that the power spectrum analysis
does not depend on the choice of redshift bin
and may be treated as additional evidence
for the existence of the peak-depression
structure discussed above on the significance level
(~4s).
The distribution obtained can be imagined as a series of embedded spheres of absorbing material (onion-like structure) corresponding to the peaks at zm indicated above. Such structure may be considered as a Global Large-Scale Structure (GLSS) of the space-time distribution, and most likely is associated with an appearance of pronounced and depressed epochs in the course of cosmological evolution.
The characteristic time T between the maxima of pronounced epochs strongly depends on the cosmological model and/or on a trial function explored. For instance, one can estimate that T=D/H0=(650±30)h-1 Myr for the trial function ln(1+z) and T=2D/H0=(400±60)h-1 Myr for the trial function (1+z)-1/2.
Let us stress that there is no contradiction between the GLSS considered and the statement that all points of space are equivalent (the cosmological principle). The GLSS does not correspond to a fixed cosmic time, but displays the time evolution. As an example of the pronounced epochs appearing as isotropic elements of the GLSS one may considered the epoch of the hydrogen recombination associated with formation of the Cosmic Microwave Background.
Most probable that GLSS should appear in statistics of other independent indicators of matter, e.g., in statistics of quasars, high-redshifted galaxies, AGNs, and so on. Comprehensive statistical analysis of QSOs and related objects is carried out just now in our Department. A plenty of preliminary distributions have been calculated for this aim as a basis for following more eloborated calculations. A few illustrations of such distributions are presented in the Notebook "Quasars and Active Galactic Nuclei". We hope that the illustrations will be filled up and improved with time.
Ryabinkov A.I., Varshalovich D.A., Kaminker A.D., 1998, Astron. Lett. 24, 418
Ryabinkov A.I., Varshalovich D.A., Kaminker A.D., 1999, Gravitation & Cosmology Suppl., Proceedings of "Cosmion-96" and "Cosmion-97", Part II, p. 72.
Kaminker A.D., Ryabinkov A.I., Varshalovich D.A., 2000, Astron. Astrophys. 358, 1.