|
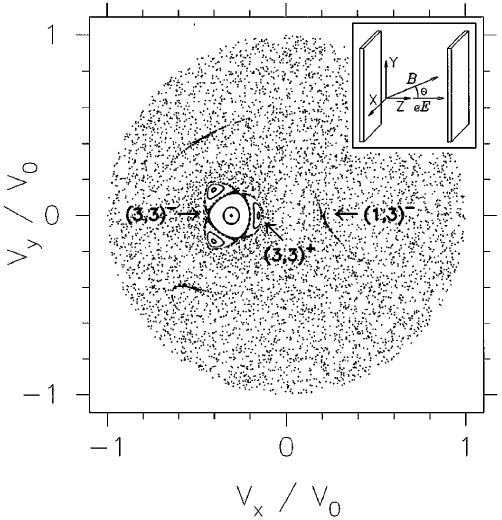
Poincaré surface of section at the collector barrier for q = 38°, b = 3.7° , g = 1.17° .
The axes are the scaled velocities in the plane transverse to the electric field (see inset). The positions of one of the three fixed points of
different period-three orbits are indicated by arrows (others are symmetrically placed). Note that a large period-one
stable island near the center of the SOS also leads to strong localization of the quantum wave functions by the familiar
procedure of local torus quantization. Because of its isolation from the relevant unstable PO’s these stable contributions can
be easily distinguished from scars. The inset shows a schematic of the geometry with our axis conventions.
|
|
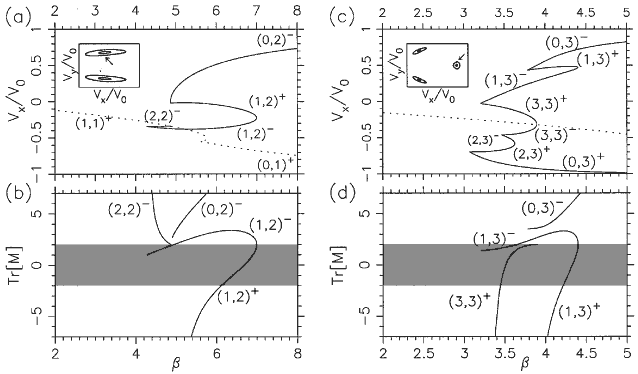
Bifurcation diagrams for the relevant period-two (a) and period-three (c) orbits. The axis b (defined in text)
may be regarded as the scaled magnetic field; the vertical axis is the ux coordinate of one of the fixed points in the SOS
associated with the orbit as indicated by the arrow in the inset.
( b), (d ) Plots of the trace of the monodromy (stability) matrix for the corresponding orbits; shaded area (
|Tr[Mg]| < 2 denotes stability region. Orbits denoted (1,2)-,
(1,3)- remain slightly unstable over a large variation of
b , leading to strong scarring. The notation ( m, n )±
used for the periodic orbits represents the topology of the orbit
( m collisions with the emitter barrier and n collisions with the collector
barrier per period; +, - indicates that the orbit is stable, unstable just before its disappearance by inverse bifurcation).
|
|
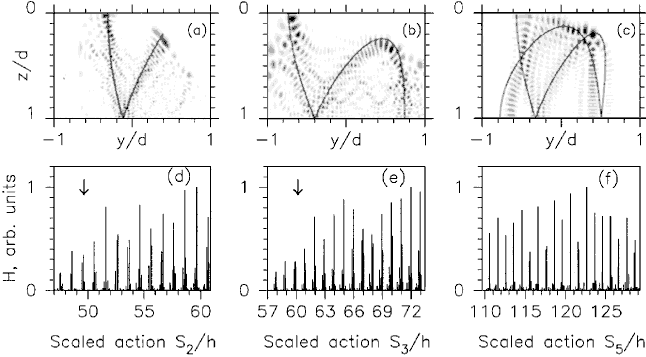
(a)-(c) Examples of wave functions scarred by unstable (1,2)- orbit (a),
(1,3)- orbit (b), and (1,5)- orbit (c);
y-z projections of orbits are superimposed.
(d)-(f) "Scar strength" H vs the scaled action S(en)/h of the unstable
orbit which scars the eigenstate of energy en.
The three cases shown are (a) (1,2)- orbit, ( b) (1,3)- orbit, (c) (1,5)- orbit.
The arrows indicate the values of b for the tangent bifurcation, which give birth to the periodic orbits.
Note that when increasing action (or energy) the tangent bifurcation at higher
b ~ 1/e occurs at the lower action side.
The peaks of the scar strength below the tangent bifurcation are due to the "ghost effect".
Scaled actions below the bifurcation points were obtained by linear extrapolation of the (approximately linear) function.
|


